In the old days we were happy with mean field approximation. Currently we don't. As the model goes more complicated, Bayesian inference needs more accurate yet fast approximations to the exact posterior, and apparently mean-field is not a very good choice. To enhance the power of variational approximations people start to use invertible transformations (e.g. see the normalizing flow paper) that warp simple distributions (e.g. factorised Gaussian) to complicated ones that are still differentiable. However it introduces an extra cost: you need to be able to compute the determinant of the Jacobian of that transform in a fast way. Solutions of this include constructing the transform with a sequence of "simple" functions -- simple in the sense that the Jacobian is low-rank or triangular (e.g. see this paper). Recently I found a NIPS preprint that provides another solution of this, which is absolutely amazing: through their clever design you don't even need to compute the Jacobian at all! I found this paper a very interesting read so I decided to put a blog post here:
Stein Variational Gradient Descent: A General Purpose Bayesian Inference Algorithm
Qiang Liu and Dilin Wang
http://arxiv.org/abs/1608.04471 (to appear at NIPS 2016)
You might also want to check out their previous work at this year's ICML.
Before going to the details, let's recap the idea of invertible transformations of random variables. Assume 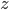 is a random variable distributed as
is a random variable distributed as 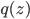 , e.g. Gaussian. Now if a mapping
, e.g. Gaussian. Now if a mapping 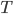 is differentiable and invertible, then the transformation
is differentiable and invertible, then the transformation 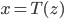 is also a random variable, distributed as (using notations in the paper)
is also a random variable, distributed as (using notations in the paper) 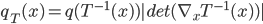 . If we use this distribution in VI, then the variational free energy becomes
. If we use this distribution in VI, then the variational free energy becomes ![\mathrm{KL}[q_T(x)||p(x|\mathcal{D})] - \log p(\mathcal{D})](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_4f4cf9ee67b0075216141f37d71cfe14.gif) , which means we need to evaluate the log determinant of the Jacobian
, which means we need to evaluate the log determinant of the Jacobian 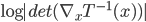 . As said
. As said 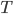 often contains a sequence of "simple" mappings, in math this is
often contains a sequence of "simple" mappings, in math this is 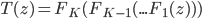 , so the determinant term becomes
, so the determinant term becomes 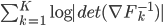 .
.
Previous approaches parameterised the 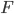 functions with carefully designed neural networks, and optimised all these network parameters jointly through the free energy. This paper, although not explicitly mentioned, used sequential optimisation instead: it first finds
functions with carefully designed neural networks, and optimised all these network parameters jointly through the free energy. This paper, although not explicitly mentioned, used sequential optimisation instead: it first finds 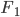 by minimising the energy, then fixes it and proceeds to
by minimising the energy, then fixes it and proceeds to 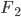 and so on. No fine-tuning at the end. Now optimisation becomes easier, but potentially you need more transformations and thus longer training time in total. Also storing these functions can be very challenging for memory.
and so on. No fine-tuning at the end. Now optimisation becomes easier, but potentially you need more transformations and thus longer training time in total. Also storing these functions can be very challenging for memory.
To solve these problems the authors proposed using functional gradients. They assumed a very simple form for the transform: 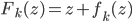 where
where 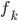 belongs to some RKHS defined by a kernel
belongs to some RKHS defined by a kernel 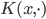 , and used functional gradients to find the
, and used functional gradients to find the 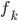 function. Then instead of finding a local optimum of
function. Then instead of finding a local optimum of 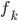 , we can do "early stopping", or even just run one gradient step, then move to the next transform. Furthermore, if you start your search at
, we can do "early stopping", or even just run one gradient step, then move to the next transform. Furthermore, if you start your search at 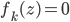 , then there's no need to evaluate the determinant as now
, then there's no need to evaluate the determinant as now 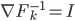 ! This solves the running time problem even when we need much more of these transforms compared to previous approaches. Another nice explanation is that now
! This solves the running time problem even when we need much more of these transforms compared to previous approaches. Another nice explanation is that now 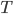 becomes
becomes 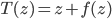 with
with 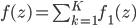 , and if the norm of
, and if the norm of 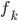 is small enough, then the above is also equivalent to one gradient step for
is small enough, then the above is also equivalent to one gradient step for 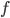 at point
at point 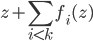 . I like both ways of interpreting this procedure and I would say it comes from the clever design of the sequential transform.
. I like both ways of interpreting this procedure and I would say it comes from the clever design of the sequential transform.
The authors provided the analytical form of this functional gradient which links back to the kernel Stein discrepancy discussed in their ICML paper:
![\nabla_{f_k} \mathrm{KL}[q_{F_k} || p] |_{f_k = 0} = - \mathbb{E}_{z \sim q} [ \nabla_z K(z, \cdot) + \nabla_z \log p(z) K(z, \cdot) ]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_0fbcda61d26647608f017b8ea8003a8e.gif) ,
,
where 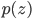 short-hands the joint distribution
short-hands the joint distribution 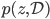 . Since now Monte Carlo estimation has become quite a standard approach for modern VI, we can use samples from the
. Since now Monte Carlo estimation has become quite a standard approach for modern VI, we can use samples from the 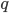 distribution to compute the above gradient. Assume we take
distribution to compute the above gradient. Assume we take 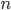 samples
samples 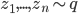 . By taking only one gradient step with learning rate
. By taking only one gradient step with learning rate 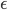 the current transform becomes
the current transform becomes ![F_k(z) = z + \frac{\epsilon}{n} \sum_n [ \nabla_{z_n} K(z_n, z) + \nabla_{z_n} \log p(z_n) K(z_n, z) ]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_458400379ef4b630d2b0e17fa3f81bf3.gif) . We can also use mini-batches to approximate
. We can also use mini-batches to approximate 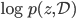 to make the algorithm scalable on large datasets. In fact they reported even faster speed than PBP on Bayesian neural network with comparable results to the state-of-the-art, which looks very promising.
to make the algorithm scalable on large datasets. In fact they reported even faster speed than PBP on Bayesian neural network with comparable results to the state-of-the-art, which looks very promising.
After the gradient step of 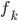 , the algorithm moves to the next transform
, the algorithm moves to the next transform 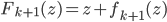 and again starts at
and again starts at 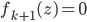 . Notice now the
. Notice now the 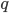 distribution that we simulate
distribution that we simulate 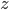 from in the above gradient equation becomes
from in the above gradient equation becomes 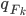 , which do contain a non-identity Jacobian if we want to evaluate it directly. However recall the core idea of invertible transformation that we can simulate
, which do contain a non-identity Jacobian if we want to evaluate it directly. However recall the core idea of invertible transformation that we can simulate 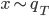 by first sample
by first sample 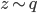 then apply
then apply 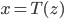 , and we do have samples from
, and we do have samples from 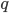 from the last step. This means we can first apply the transform to update the samples (with Monte Carlo estimate)
from the last step. This means we can first apply the transform to update the samples (with Monte Carlo estimate) ![z_i \leftarrow z_i + \frac{\epsilon}{n} \sum_n [ \nabla_{z_n} K(z_n, z_i) + \nabla_{z_n} \log p(z_n) K(z_n, z_i) ]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_01ecec148b3831efa3956017d93cded4.gif) , then use them to compute this step's gradient. It makes the algorithm sampling-like and the memory consumption only comes from storing these samples, which can be very cheap compared to storing lots of parametric functionals. If one is still unhappy with storing samples (say due to limited memory), one can fit a parametric density to the samples after the last transform
, then use them to compute this step's gradient. It makes the algorithm sampling-like and the memory consumption only comes from storing these samples, which can be very cheap compared to storing lots of parametric functionals. If one is still unhappy with storing samples (say due to limited memory), one can fit a parametric density to the samples after the last transform 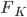 . Another strategy is to only use 1 sample, and in this case this algorithm reduces to maximum a posteriori (MAP), which still finds a mode of posterior for you.
. Another strategy is to only use 1 sample, and in this case this algorithm reduces to maximum a posteriori (MAP), which still finds a mode of posterior for you.
The authors used RBF kernel and also pointed out that this algorithm also recovers MAP when the bandwidth tends to zero. This make sense as you can understand it through analogies of kernel density estimation, and in general running VI with 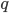 as a delta function is also equivalent to MAP. In other words, the number of samples
as a delta function is also equivalent to MAP. In other words, the number of samples 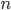 and the kernel implicitly define the family of variational distribution
and the kernel implicitly define the family of variational distribution 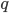 : the kernel mainly controls the smoothness, and the number of samples roughly indicates the complexity of your fit. Presumably the main criticism I have is also from the nature that
: the kernel mainly controls the smoothness, and the number of samples roughly indicates the complexity of your fit. Presumably the main criticism I have is also from the nature that 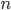 affects the complexity of
affects the complexity of 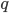 , which is not the case for other black-box VI techniques. This means in high dimensions where using large number of samples has prohibitive memory cost, you need to carefully tune the kernel parameters in order to get a good fit, or even you might not be able to achieve significantly better results than MAP. Well using mean-field Gaussian in high-dimensions also seems insufficient, but at least the community has relatively clear understanding in this case. For this method it's unclear to me right now what the distribution looks like and whether it is often better than mean-field. Perhaps I should raise this questions to the authors and I’ll be very excited to hear more about it from their poster at NIPS!
, which is not the case for other black-box VI techniques. This means in high dimensions where using large number of samples has prohibitive memory cost, you need to carefully tune the kernel parameters in order to get a good fit, or even you might not be able to achieve significantly better results than MAP. Well using mean-field Gaussian in high-dimensions also seems insufficient, but at least the community has relatively clear understanding in this case. For this method it's unclear to me right now what the distribution looks like and whether it is often better than mean-field. Perhaps I should raise this questions to the authors and I’ll be very excited to hear more about it from their poster at NIPS!
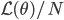
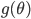
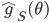
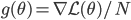

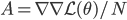
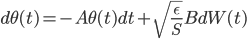
![q(\theta) \propto \exp \left[-\frac{1}{2} \theta^T \Sigma^{-1} \theta \right]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_1dd4e70879ab877ee2b3ed2b2dc7c262.gif)
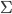
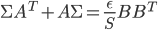
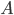
![\mathrm{KL}[q(\theta)||p(\theta|x_1, ..., x_N)]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_688b54f4781d9080e5cf384f0b175b64.gif)
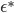
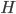
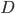
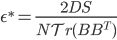
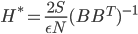
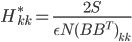
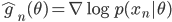
![I(\theta) = \mathbb{E}_x[\nabla \log p(x|\theta)^2]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_92488f0955aa08b95f4f9dc0ae6297e5.gif)
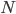
![I(\theta) = \mathbb{E}_x[-\nabla \nabla \log p(x|\theta)] = \lim_{N \rightarrow +\infty} \nabla \nabla \mathcal{L}(\theta) / N](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_eedda9e4535ffba1657000de3726a5e2.gif)
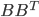
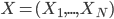
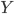
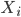
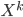
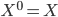
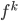
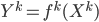
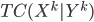
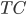
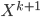
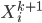
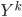
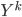
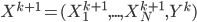
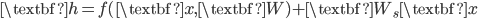
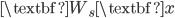
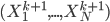
![[\textbf{W}_s \textbf{x}, f(\textbf{x}, \textbf{W})]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_de056466e2af0f1a1b14af9ca4413413.gif)
![\textbf{W}(\textbf{a} + \textbf{b}) = [\textbf{W}, \textbf{W}] [\textbf{a}^T, \textbf{b}^T]^T](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_ef5b3439cb08d522eba7459de095dccd.gif)