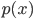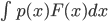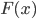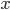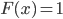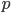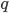Topics in approximate inference

To me, approximate inference finds the best approximation to an integration problem confronting computational constraints.

Imagine you have a distribution $p(x)$ and you want to compute the integral $\int p(x) F(x) dx$ for some function $F(x)$ of interest. We call the computation of this integral as inference. Examples include Bayesian inference where now $p(x)$ is some posterior distribution and $F(x)$ is the likelihood function of $x$ on unseen data. Or if $p(x)$ is unnormalised, taking $F(x) = 1$ would return the integral as the normalising constant (or partition function) of $p$. Unfortunately for many complicated models we are fancy on now (say neural networks) this integral is intractable, and here intractability means you can't compute the exact value of the integral due to computational constraints (say running time, memory usage, precision, etc). So instead we use approximate inference to approximate that integral.

Now you might ask: why I should care about this approximate integral in the first place? Couldn't we just forget about integrals and do point estimations instead? Or couldn't we just use models that can do exact inference (e.g. stacking invertible transformations, auto-regressive models, sum-product networks)? Well for the first question it's more like a debate between Frequentist and Bayesian which I don't think I should say too much about it here. But I shall emphasize that integration is almost everywhere in probability and statistics, say calculating expectations and computing marginal distributions. For the second question, those models are usually more computationally demanding (both in time and memory), which is exactly the point for not using them and do approximate inference instead if you don't have that much computational resource. Approximate inference only makes sense when you do have computational constraints, and the way you do approximate inference also depends on how much precision you want and computational resource you have.

There are mainly two ways to do approximate inference: directly approximating the integral you want, or, finding an accurate approximation 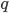$q$ to the target distribution 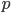$p$ and using it for integration later. The first approach is mainly dominated by sampling methods (and maybe adding student models to distill it) and quadrature. The second one, sometimes referred as the indirect approach, will be the focus of this list.